Last Formel
'Last Formel' ist in der PRO-Version für die Payload, Thrust & Kraft/Drehmoment-Formel sowie in der Fr-, Fa-, rUL- und mUL-Formel für den Rotierendmechanismus verfügbar.

Erstellen Sie eine Lastformel, um komplexe dynamische Lasten zu modellieren, die ein Funktion von Position, Entfernung, Geschwindigkeit, Beschleunigung und Zeit sein können. In der Tabelle unten werden die Variablen, Rechenarten und Funktionen aufgeführt, die bei der Erstellung einer Lastformel für eine Last verwendet werden können.

Formel Textbox

In der Formel Textbox mit der rechten Maustaste klicken, und ein Dropdown-Menü angezeigt, in das Profil Variablen, Konstanten, arithmetische, Vergleiche und math-Funktionen.
Einheiten für das Formelergebnis

Einheiten für die in der Formel verwendeten Variablen

 

Zeit

  

ZSEG, ZGES, ZCYC, ZSEGG, ZGESG, ZCYCG
 

Weg

  

DSEG, DMOV, DCYC, etc.
 

Geschwindigkeit

  

GES, MAXGES, MAXGESZYC
 

Beschl

  

BES

 

Beispiele:

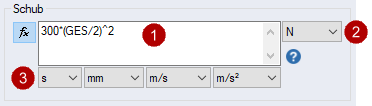
1. Erstellen Sie eine einfache Schubformel; bei der der Schub 100 mal das Quadrat der Geschwindigkeit beträgt:

2. Erstellen Sie ein etappenweises Schubprofil unter Verwendung der Formel:

 

In der Formel Textbox mit der rechten Maustaste klicken, und ein Dropdown-Menü angezeigt, in das Profil Variablen, Konstanten, arithmetische, Vergleiche und math-Funktionen.

Profilvariablen Diagramm

Profilvariablen Einheiten
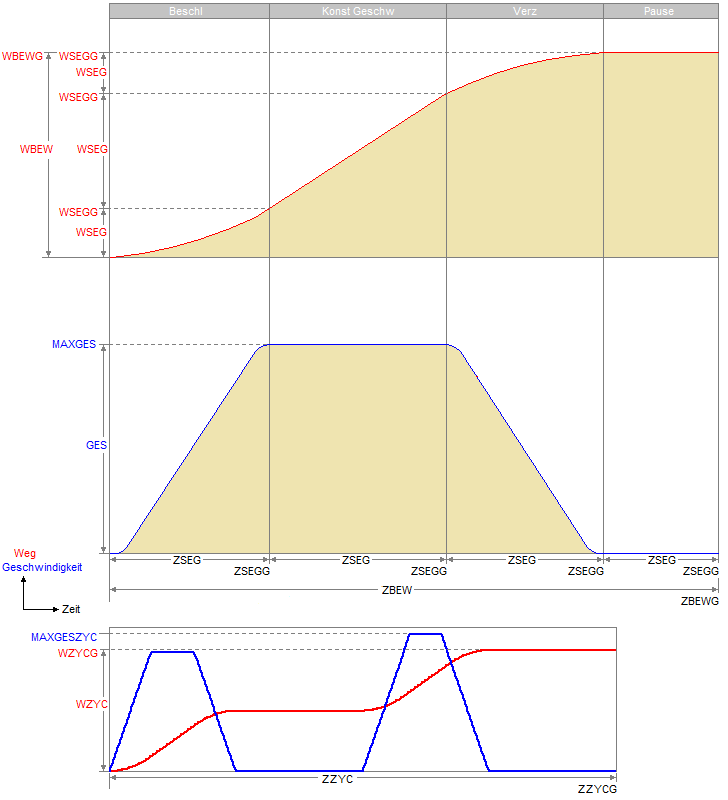
WSEG Entfernung im Abschnitt Linear: m, mm, in
Rotierend: °, rad, U
WBEW Entfernung in der Bewegung Linear: m, mm, in
Rotierend: °, rad, U
WZYC Entfernung im Zyklus/Sequenz Linear: m, mm, in
Rotierend: °, rad, U
WSEGG Entfernung Abschnitt Gesamt Linear: m, mm, in
Rotierend: °, rad, U
WBEWG Entfernung Bewegung Gesamt Linear: m, mm, in
Rotierend: °, rad, U
WZYCG Entfernung Zyklus/Sequenz Gesamt Linear: m, mm, in
Rotierend: °, rad, U
GES Geschwindigkeit Linear: m/s, mm/s, in/s
Rotierend: °/s, rad/s, rev/s
MAXGES Maximum Geschwindigkeit im Abschnitt/Bewegung
Immer ein positiver Wert
Dh. MAXGES = Max(Abs(GES)) im Abschnitt/Bewegung		 Linear: m/s, mm/s, in/s
Rotierend: °/s, rad/s, rev/s
MAXGESZYC Maximum Geschwindigkeit im Zyklus/Sequenz
Immer ein positiver Wert
Dh. MAXGESZYC = Max(Abs(GES)) im Zyklus/Sequenz		 Linear: m/s, mm/s, in/s
Rotierend: °/s, rad/s, rev/s
BES Beschleunigung Linear: m/s2, mm/s2, in/s2
Rotierend: °/s2, rad/s2, rev/s2
ZSEG Zeit im Abschnitt s
ZBEW Zeit in der Bewegung s
ZZYC Zeit im Zyklus/Sequenz s
ZSEGG Zeit Abschnitt Gesamt s
ZBEWG Zeit Bewegung Gesamt s
ZZYCG Zeit Zyklus/Sequenz Gesamt s
  
Konstanten
PI Pi (3.14159265358979...)
  
Rechenarten
+ Addition
- Subtraktion
* Multiplikation
/ Division
\ Ganzzahldivision
^ Exponentiation (Erhöhung auf eine Leistung von)
Mod

Arithmetischer Teilungsrest

  5 Mod 2 = 1
  5 Mod -2 = 1
  -5 Mod -2 = 1
  -5 Mod 2 = -1
  Abs(-5 Mod 2) = 1
Wenn Multiplikations- und Divisionsvorgänge in einem Ausdruck gemeinsam vorkommen, wird jede Operation so, wie sie auftritt, von links nach rechts berechnet. Gleichermaßen werden, wenn Additionen und Subtraktionen in einem Ausdruck gemeinsam vorkommen, alle Operationen in der Reihenfolge ihres Auftretens von links nach rechts berechnet.
 
Vergleich
= Gleichheit
<> Ungleichheit
< Kleiner als
> Größer als
<= Kleiner oder gleich
>= Größer oder gleich
Is Objektäquivalenz

Wenn der Vergleich wahr ist, ist das Ergebnis der Wert 1.  Eg. (3>2)=1

Wenn der Vergleich falsch ist, ist das Ergebnis der Wert 0.  Eg. (1>2)=0
  
Mathematische Funktionen Einheiten
Abs Absolutwert
Bsp. Abs(-1)=1
Atn Arkustangens
Bsp. Atn(1)=PI/4
Cos Cosinuswert eines Winkels
Bsp. Cos(PI/4)=0.707106781...		 [rad]
Exp e erhöht auf eine Leistung
Bsp. Exp(1)=e=2.718281828459...
Log Natürlicher Logarithmus
Kann kombiniert werden, um den Log einer
jeden Basis n zu erzeugen.
Bsp. Logn(x) = Log(x) / Log(n)
Sgn Signum = Zeichen einer Zahl
x>0: Sgn(x)=1, x=0: Sgn(x)=0, x<0: Sgn(x)=-1
Sin Sinuswert eines Winkels
Bsp. Sin(PI/4)=0.707106781...		 [rad]
Sqr Quadratwurzel
Bsp. Sqr(9)=9^½=3
Tan Tangenswert eines Winkels
Bsp. Tan(PI/4)=1		 [rad]
Int Ganzzahliger Anteil einer Zahl1  
Fix Ganzzahliger Anteil einer Zahl1  
1Der Unterschied zwischen Int und Fix besteht darin, dass Int bei einer negativen Zahl die erste negative ganze Zahl, wiedergibt, die kleiner oder gleich der Zahl ist, Fix dagegen die erste negative ganze Zahl, die größer oder gleich der Zahl ist. So wandelt z. B. Int -8,4 in -9 um, während Fix für -8,4 -8 liefert.
 
Logik
And Logische Verknüpfung
Not Logische Verneinung
Or Logische Disjunktion
Xor Logischer Ausschluss
Eqv Logische Äquivalenz
Imp Logische Implikation
 

 

Abgeleitete Mathematische Funktionen
Secans Sec(X) = 1 / Cos(X)
Cosecans Cosec(X) = 1 / Sin(X)
Cotangens Cotan(X) = 1 / Tan(X)
Arcussinus Arcsin(X) = Atn(X / Sqr(-X * X + 1))
Arcuscosinus Arccos(X) = Atn(-X / Sqr(-X * X + 1)) + 2 * Atn(1)
Arcussecans Arcsec(X) = 2 * Atn(1) – Atn(Sgn(X) / Sqr(X * X – 1))
Arcuscosecans Arccosec(X) = Atn(Sgn(X) / Sqr(X * X – 1))
Arcuscotangens Arccotan(X) = 2 * Atn(1) - Atn(X)
Sinus hyperbolicus HSin(X) = (Exp(X) – Exp(-X)) / 2
Cosinus hyperbolicus HCos(X) = (Exp(X) + Exp(-X)) / 2
Tangens hyperbolicus HTan(X) = (Exp(X) – Exp(-X)) / (Exp(X) + Exp(-X))
Secans hyperbolicus HSec(X) = 2 / (Exp(X) + Exp(-X))
Cosecans hyperbolicus HCosec(X) = 2 / (Exp(X) – Exp(-X))
Cotangens hyperbolicus HCotan(X) = (Exp(X) + Exp(-X)) / (Exp(X) – Exp(-X))
Arcussinus hyperbolicus HArcsin(X) = Log(X + Sqr(X * X + 1))
Arcuscosinus hyperbolicus HArccos(X) = Log(X + Sqr(X * X – 1))
Arcustangens hyperbolicus HArctan(X) = Log((1 + X) / (1 – X)) / 2
Arcussecans hyperbolicus HArcsec(X) = Log((Sqr(-X * X + 1) + 1) / X)
Arcuscosecans hyperbolicus HArccosec(X) = Log((Sgn(X) * Sqr(X * X + 1) + 1) / X)
Arcuscotangens hyperbolicus HArccotan(X) = Log((X + 1) / (X – 1)) / 2
Logarithmus zur Basis N LogN(X) = Log(X) / Log(N)

 

Verwandte Themen