Getriebe Wirkungsgrad gegen Eingangsdrehzahl

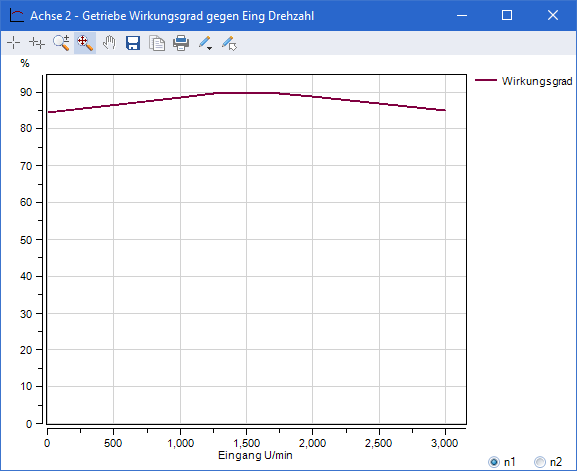
Bei den meisten Getriebemodellen variiert der Wirkungsgrad je nach Drehzahl. Die meisten Hersteller geben allerdings einen einzelnen Wirkungsgrad-Nennwert für alle Drehzahlen an. In den meisten Fällen ist dies ausreichend, wenn der Wirkungsgrad über den gesamten Drehzahlbereich nur leicht variiert. Bei manchen Getriebekonstruktionen treten jedoch über den Drehzahlbereich hinweg beträchtliche Wirkungsgradschwankungen auf. Die Gegenüberstellung von Wirkungsgrad und Eingangsdrehzahl dient zur Berechnung des für bestimmte Drehzahlen konkret geltenden Wirkungsgrads. Auf diese Weise sind alle Leistungsberechnungen präziser und benötigen keine Schätzungen oder Anpassungen durch den Anwender.

Wenn das gewählte Getriebe die Wirkungsgrad-Formel verwendet und in der Formel die Variable [T] vorkommt, wird der Drehmoment-Wert T2 auch beim Getriebewirkungsgrad angezeigt.

Effizienz 7-Punkte-Kurve und Effizienzformel

Seit v2 wurde der Getriebewirkungsgrad in der Datenbank durch eine Kennlinie mit 7 Stützpunkten (Eingangsdrehzahl, Wirkungsgrad) festgelegt. Die Wirkungsgradkennlinie wird typischerweise auf das Nenn-Ausgangsmoment des Getriebes bezogen. Die 7-Punkt-Kennlinie ist für die meisten Getriebe ausreichend exakt.

Die Wirkungsgrad-Formel [Eff_Frml], die in v4.6 eingeführt wurde, ermöglicht die Berechnung des Getriebewirkungsgrades basierend auf den Variablen Eingangsdrehazhl [n] und Ausgangsdrehmoment [T]. Die Formel kann bis zu 500 Zeichen umfassen. Die Formel ist optional, wenn sie nicht vorgegeben ist, wird die Wirkungsgradkennlinie verwendet.

Formel Variablen, Bedingungen, Funktionen etc.

Die Getriebe-Wirkungsgradformel kann jeden der folgenden Ausdrücke verwenden:

Formelvariablen

Einheiten

Eingangsdrehzahl

rpm

Ausgangsmoment

Konstanten

Pi (3.14159265358979...)

Rechenarten

Addition

Subtraktion

Multiplikation

Division

Ganzzahldivision

Exponentiation (Erhöhung auf eine Leistung von)

Mod

Arithmetischer Teilungsrest

5 Mod 2	=	1
5 Mod -2	=	1
-5 Mod -2	=	1
-5 Mod 2	=	-1
Abs(-5 Mod 2)	=	1

Wenn Multiplikations- und Divisionsvorgänge in einem Ausdruck gemeinsam vorkommen, wird jede Operation so, wie sie auftritt, von links nach rechts berechnet. Gleichermaßen werden, wenn Additionen und Subtraktionen in einem Ausdruck gemeinsam vorkommen, alle Operationen in der Reihenfolge ihres Auftretens von links nach rechts berechnet.

Vergleich

Gleichheit

Ungleichheit

Kleiner als

Größer als

Kleiner oder gleich

Größer oder gleich

Objektäquivalenz

Wenn der Vergleich wahr ist, ist das Ergebnis der Wert 1. Eg. (3>2)=1

Wenn der Vergleich falsch ist, ist das Ergebnis der Wert 0. Eg. (1>2)=0

Mathematische Funktionen

Einheiten

Abs

Absolutwert
Bsp. Abs(-1)=1

Atn

Arkustangens
Bsp. Atn(1)=PI/4

Cos

Cosinuswert eines Winkels
Bsp. Cos(PI/4)=0.707106781...

[rad]

Exp

e erhöht auf eine Leistung
Bsp. Exp(1)=e=2.718281828459...

Log

Natürlicher Logarithmus
Kann kombiniert werden, um den Log einer
jeden Basis n zu erzeugen.
Bsp. Logn(x) = Log(x) / Log(n)

Sgn

Signum = Zeichen einer Zahl
x>0: Sgn(x)=1, x=0: Sgn(x)=0, x<0: Sgn(x)=-1

Sin

Sinuswert eines Winkels
Bsp. Sin(PI/4)=0.707106781...

[rad]

Sqr

Quadratwurzel
Bsp. Sqr(9)=9^½=3

Tan

Tangenswert eines Winkels
Bsp. Tan(PI/4)=1

[rad]

Int

Ganzzahliger Anteil einer Zahl¹

Fix

Ganzzahliger Anteil einer Zahl¹

¹Der Unterschied zwischen Int und Fix besteht darin, dass Int bei einer negativen Zahl die erste negative ganze Zahl, wiedergibt, die kleiner oder gleich der Zahl ist, Fix dagegen die erste negative ganze Zahl, die größer oder gleich der Zahl ist. So wandelt z. B. Int -8,4 in -9 um, während Fix für -8,4 -8 liefert.

Logik

And

Logische Verknüpfung

Not

Logische Verneinung

Logische Disjunktion

Xor

Logischer Ausschluss

Eqv

Logische Äquivalenz

Imp

Logische Implikation

Abgeleitete Mathematische Funktionen
Secans	Sec(X) = 1 / Cos(X)
Cosecans	Cosec(X) = 1 / Sin(X)
Cotangens	Cotan(X) = 1 / Tan(X)
Arcussinus	Arcsin(X) = Atn(X / Sqr(-X * X + 1))
Arcuscosinus	Arccos(X) = Atn(-X / Sqr(-X * X + 1)) + 2 * Atn(1)
Arcussecans	Arcsec(X) = 2 * Atn(1) – Atn(Sgn(X) / Sqr(X * X – 1))
Arcuscosecans	Arccosec(X) = Atn(Sgn(X) / Sqr(X * X – 1))
Arcuscotangens	Arccotan(X) = 2 * Atn(1) - Atn(X)
Sinus hyperbolicus	HSin(X) = (Exp(X) – Exp(-X)) / 2
Cosinus hyperbolicus	HCos(X) = (Exp(X) + Exp(-X)) / 2
Tangens hyperbolicus	HTan(X) = (Exp(X) – Exp(-X)) / (Exp(X) + Exp(-X))
Secans hyperbolicus	HSec(X) = 2 / (Exp(X) + Exp(-X))
Cosecans hyperbolicus	HCosec(X) = 2 / (Exp(X) – Exp(-X))
Cotangens hyperbolicus	HCotan(X) = (Exp(X) + Exp(-X)) / (Exp(X) – Exp(-X))
Arcussinus hyperbolicus	HArcsin(X) = Log(X + Sqr(X * X + 1))
Arcuscosinus hyperbolicus	HArccos(X) = Log(X + Sqr(X * X – 1))
Arcustangens hyperbolicus	HArctan(X) = Log((1 + X) / (1 – X)) / 2
Arcussecans hyperbolicus	HArcsec(X) = Log((Sqr(-X * X + 1) + 1) / X)
Arcuscosecans hyperbolicus	HArccosec(X) = Log((Sgn(X) * Sqr(X * X + 1) + 1) / X)
Arcuscotangens hyperbolicus	HArccotan(X) = Log((X + 1) / (X – 1)) / 2
Logarithmus zur Basis N	LogN(X) = Log(X) / Log(N)

Beispiel für eine Formel, die Excel Trendlinie nutzt

Dies ist ein Beispiel, wie man eine Wirkungsgradformel basierend auf Drehzahl und Drehmoment erstellt, indem man Excel mit dem Feature Trendlinie benutzt.

Geben Sie Eingangsdrehzahl und Wirkungsgraddaten in Excel ein wie in Spalte A und B gezeigt. Je mehr Punkte desto genauer wird die Formel für die Trendlinie sein.
Erzeugen Sie ein Punkte-Diagramm aus diesen Daten
Fügen Sie eine Trendlinie als Polynom 6. Grades hinzu.
Sehen Sie ausreichend viele Nachkommastellen für die Trendlinie vor, um die Genauigkeit der Formel sicherzustellen.
Dann markieren und kopieren Sie den Text der Trendlinien-Formel und übertragen ihn in eine Test-Zelle wie gezeigt (B17).
Ersetzen Sie die "x" mit Test-Zelle "A17" und fügen Sie das Zeichen "^" für den Exponenten ein, wo nötig.
Testen Sie die Formel um sicherzustellen dass sie richtig funktioniert.
Wiederholen Sie die obigen Schritte mit einer zweiten Tabelle und Diagramm, diesmal für das Ausgangsdrehmoment.

Schließlich ändern Sie die Zellbezüge in die Variablen [n] und [T] und verwenden Sie die Formel in der Datenbank für das Getriebe.

Das Endergebnis ist die folgende Formel, die in der Datenbank verwendet werden kann:

n_Frml	-2.4111892925777E-21n^6 + 2.03381955062493E-17n^5 - 5.75882852880029E-14n^4 + 5.44844700768859E-11n^3 - 1.25747901258411E-08n^2 + 0.0000423701080478622n + 0.845017800146564
T_Frml	-5.43888519147239E-17T^6 + 1.65674844019666E-13T^5 - 2.01826688177922E-10T^4 + 1.24626454993566E-07T^3 - 0.0000411676222198398T^2 + 0.00700356844846084T + 0.498005569090196
Eff_Frml	(n_Frml)(T_Frml) (-2.4111892925777E-21n^6 + 2.03381955062493E-17n^5 - 5.75882852880029E-14n^4 + 5.44844700768859E-11n^3 - 1.25747901258411E-08n^2 + 0.0000423701080478622n + 0.845017800146564) (-5.43888519147239E-17T^6 + 1.65674844019666E-13T^5 - 2.01826688177922E-10T^4 + 1.24626454993566E-07T^3 - 0.0000411676222198398T^2 + 0.00700356844846084T + 0.498005569090196)

Getriebe Wirkungsgrad gegen Eingangsdrehzahl

Effizienz 7-Punkte-Kurve und Effizienzformel

Formel Variablen, Bedingungen, Funktionen etc.

Beispiel für eine Formel, die Excel Trendlinie nutzt

Excel: Input Speed vs Efficiency

Excel: Output Torque vs Efficiency

Excel: Trendline Options & Numeric Format

Verwandte Themen