| Formula Variables
|
Units
|
| n |
Input Speed |
rpm |
| T |
Output Torque |
Nm |
| |
| Constants
|
| PI |
Pi (3.14159265358979...) |
| |
| Arithmetic
|
| + |
Addition |
| - |
Subtraction |
| * |
Multiplication |
| / |
Division |
| \ |
Integer division |
| ^ |
Exponentiation (raise to a power of) |
| Mod |
Modulus arithmetic
| |
5 Mod 2 |
= |
1 |
| |
5 Mod -2 |
= |
1 |
| |
-5 Mod -2 |
= |
1 |
| |
-5 Mod 2 |
= |
-1 |
| |
Abs(-5 Mod 2) |
= |
1 |
|
| When multiplication and division occur together in
an expression, each operation is evaluated as it occurs from left
to right. Likewise, when addition and subtraction occur together in
an expression, each operation is evaluated in order of appearance
from left to right. |
| |
| Comparison
|
| = |
Equality |
| <> |
Inequality |
| < |
Less than |
| > |
Greater than |
| <= |
Less than or equal to |
| >= |
Greater than or equal to |
| Is |
Object equivalence |
|
When the comparison is True, the result value is
1. Eg. (3>2)=1
When the comparison is False, the result value is
0. Eg. (1>2)=0
|
| |
| Math Functions
|
Units
|
| Abs |
Absolute
Eg. Abs(-1)=1 |
|
| Atn |
Arctangent
Eg. Atn(1)=PI/4 |
|
| Cos |
Cosine of an angle
Eg. Cos(PI/4)=0.707106781... |
[rad] |
| Exp |
e raised to a power
Eg. Exp(1)=e=2.718281828459... |
|
| Log |
Natural logarithm
Can be combined to create the Log of any base, n.
Eg. Logn(x) = Log(x) / Log(n) |
|
| Sgn |
Sign of a number
x>0: Sgn(x)=1, x=0: Sgn(x)=0, x<0: Sgn(x)=-1 |
|
| Sin |
Sine of an angle
Eg. Sin(PI/4)=0.707106781... |
[rad] |
| Sqr |
Square root
Eg. Sqr(9)=9^½=3 |
|
| Tan |
Tangent of an angle
Eg. Tan(PI/4)=1 |
[rad] |
| Int |
Integer portion of a number1 |
|
| Fix |
Integer portion of a number1 |
|
| 1The difference between Int and Fix is
that if number is negative, Int returns the first negative integer
less than or equal to number, whereas Fix returns the first
negative integer greater than or equal to number. For example, Int
converts -8.4 to -9, and Fix converts -8.4 to -8. |
| |
| Logical
|
| And |
Logical conjunction |
| Not |
Logical negation |
| Or |
Logical disjunction |
| Xor |
Logical exclusion |
| Eqv |
Logical equivalence |
| Imp |
Logical implication |
| |
| Derived Math Functions
|
| Secant |
Sec(X) = 1 / Cos(X) |
| Cosecant |
Cosec(X) = 1 / Sin(X) |
| Cotangent |
Cotan(X) = 1 / Tan(X) |
| Inverse Sine |
Arcsin(X) = Atn(X / Sqr(-X * X + 1)) |
| Inverse Cosine |
Arccos(X) = Atn(-X / Sqr(-X * X + 1)) + 2 * Atn(1) |
| Inverse Secant |
Arcsec(X) = 2 * Atn(1) – Atn(Sgn(X) / Sqr(X * X – 1)) |
| Inverse Cosecant |
Arccosec(X) = Atn(Sgn(X) / Sqr(X * X – 1)) |
| Inverse Cotangent |
Arccotan(X) = 2 * Atn(1) - Atn(X) |
| Hyperbolic Sine |
HSin(X) = (Exp(X) – Exp(-X)) / 2 |
| Hyperbolic Cosine |
HCos(X) = (Exp(X) + Exp(-X)) / 2 |
| Hyperbolic Tangent |
HTan(X) = (Exp(X) – Exp(-X)) / (Exp(X) + Exp(-X)) |
| Hyperbolic Secant |
HSec(X) = 2 / (Exp(X) + Exp(-X)) |
| Hyperbolic Cosecant |
HCosec(X) = 2 / (Exp(X) – Exp(-X)) |
| Hyperbolic Cotangent |
HCotan(X) = (Exp(X) + Exp(-X)) / (Exp(X) – Exp(-X)) |
| Inverse Hyperbolic Sine |
HArcsin(X) = Log(X + Sqr(X * X + 1)) |
| Inverse Hyperbolic Cosine |
HArccos(X) = Log(X + Sqr(X * X – 1)) |
| Inverse Hyperbolic Tangent |
HArctan(X) = Log((1 + X) / (1 – X)) / 2 |
| Inverse Hyperbolic Secant |
HArcsec(X) = Log((Sqr(-X * X + 1) + 1) / X) |
| Inverse Hyperbolic Cosecant |
HArccosec(X) = Log((Sgn(X) * Sqr(X * X + 1) + 1) / X) |
| Inverse Hyperbolic Cotangent |
HArccotan(X) = Log((X + 1) / (X – 1)) / 2 |
| Logarithm to base N |
LogN(X) = Log(X) / Log(N) |
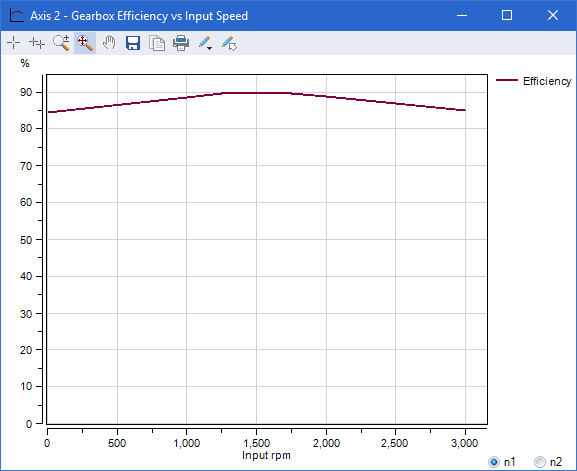
Efficiency 7
Point Curve & Efficiency Formula
Formula
Variables, Conditions, Functions, etc.
