Load Formula

'Load Formula' is available in the PRO version for the Payload, Thrust & Force/Torque formula, as well as Fr, Fa, rUL and mUL formula for the Rotary mechanism.

Create a formula to model complex dynamic loads that can be a function of position, distance, velocity, acceleration and time. The table below lists the variables, arithmetic and functions that can be used to create a load formula.

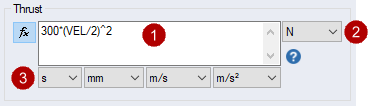
	Formula Textbox Right-click in the formula textbox, and a drop down menu appears listing the profile variables, constants, arithmetic, comparisons and math functions.
	Units for the formula result
	Units for the variables used in the formula   Time   TSEG, TMOV, TCYC, TSEGT, TMOVT, TCYCT   Distance   DSEG, DMOV, DCYC, DSEGT, DMOVT, DCYCT   Velocity   VEL, MAXVEL, MAXVELCYC   Acceleration   ACC

 

Examples:

1. Create a simple thrust function where thrust is 100 times the square of velocity:

• Thrust = 100*VEL^2
   

2. Create a Thrust Step Profile using the formula:

• Thrust = (VEL>=0 AND VEL<2)*300 + (VEL>=2)*500
  • Velocity = 0m/s, Thrust = 0N
  • 0 <= Velocity < 2m/s, Thrust = 300N
  • Velocity >= 2m/s, Thrust = 500N

 

Right-click in the formula textbox, and a drop down menu appears listing the profile variables, constants, arithmetic, comparisons and math functions.

Profile Variables Diagram

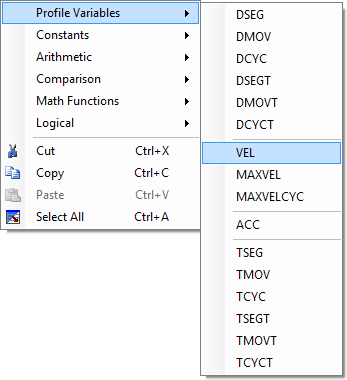
Profile Variables		Units
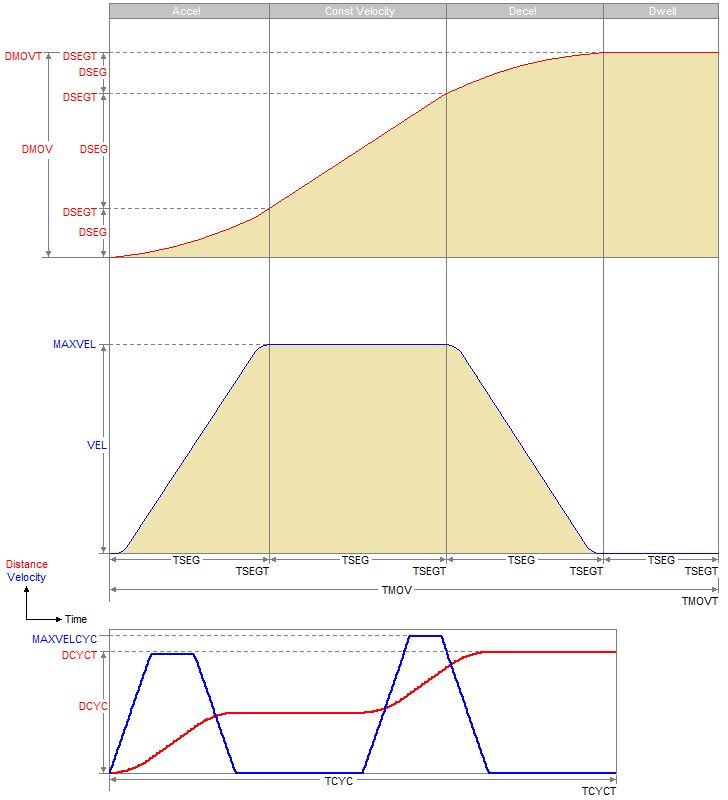
DSEG	Distance in Segment	Linear: m, mm, in Rotary: °, rad, rev
DMOV	Distance in Move	Linear: m, mm, in Rotary: °, rad, rev
DCYC	Distance in Cycle/Sequence	Linear: m, mm, in Rotary: °, rad, rev
DSEGT	Total Segment Distance	Linear: m, mm, in Rotary: °, rad, rev
DMOVT	Total Move Distance	Linear: m, mm, in Rotary: °, rad, rev
DCYCT	Total Distance of Cycle/Sequence	Linear: m,mm, in Rotary: °, rad, rev
VEL	Velocity	Linear: m/s, mm/s, in/s Rotary: °/s, rad/s, rev/s
MAXVEL	Max Velocity in Segment/Move Always a positive value Ie. MAXVEL = Max(Abs(VEL)) in the Segment/Move	Linear: m/s, mm/s, in/s Rotary: °/s, rad/s, rev/s
MAXVELCYC	Max Velocity in Cycle/Sequence Always a positive value Ie. MAXVELCYC = Max(Abs(VEL)) in the Cycle/Sequence	Linear: m/s, mm/s, in/s Rotary: °/s, rad/s, rev/s
ACC	Acceleration	Linear: m/s2, mm/s2, in/s2 Rotary: °/s2, rad/s2, rev/s2
TSEG	Time in Segment	s
TMOV	Time in Move	s
TCYC	Time in Cycle/Sequence	s
TSEGT	Total Segment Time	s
TMOVT	Total Move Time	s
TCYCT	Total Cycle/Sequence Time	s
Constants
PI	Pi (3.14159265358979...)
Arithmetic
+	Addition
-	Subtraction
*	Multiplication
/	Division
\	Integer division
^	Exponentiation (raise to a power of)
Mod	Modulus arithmetic   5 Mod 2 = 1   5 Mod -2 = 1   -5 Mod -2 = 1   -5 Mod 2 = -1   Abs(-5 Mod 2) = 1
When multiplication and division occur together in an expression, each operation is evaluated as it occurs from left to right. Likewise, when addition and subtraction occur together in an expression, each operation is evaluated in order of appearance from left to right.
Comparison
=	Equality
<>	Inequality
<	Less than
>	Greater than
<=	Less than or equal to
>=	Greater than or equal to
Is	Object equivalence
When the comparison is True, the result value is 1.  Eg. (3>2)=1 When the comparison is False, the result value is 0.  Eg. (1>2)=0
Math Functions		Units
Abs	Absolute Eg. Abs(-1)=1
Atn	Arctangent Eg. Atn(1)=PI/4
Cos	Cosine of an angle Eg. Cos(PI/4)=0.707106781...	[rad]
Exp	e raised to a power Eg. Exp(1)=e=2.718281828459...
Log	Natural logarithm Can be combined to create the Log of any base, n. Eg. Logn(x) = Log(x) / Log(n)
Sgn	Sign of a number x>0: Sgn(x)=1, x=0: Sgn(x)=0, x<0: Sgn(x)=-1
Sin	Sine of an angle Eg. Sin(PI/4)=0.707106781...	[rad]
Sqr	Square root Eg. Sqr(9)=9^½=3
Tan	Tangent of an angle Eg. Tan(PI/4)=1	[rad]
Int	Integer portion of a number1
Fix	Integer portion of a number1
1The difference between Int and Fix is that if number is negative, Int returns the first negative integer less than or equal to number, whereas Fix returns the first negative integer greater than or equal to number. For example, Int converts -8.4 to -9, and Fix converts -8.4 to -8.
Logical
And	Logical conjunction
Not	Logical negation
Or	Logical disjunction
Xor	Logical exclusion
Eqv	Logical equivalence
Imp	Logical implication

 

Derived Math Functions
Secant	Sec(X) = 1 / Cos(X)
Cosecant	Cosec(X) = 1 / Sin(X)
Cotangent	Cotan(X) = 1 / Tan(X)
Inverse Sine	Arcsin(X) = Atn(X / Sqr(-X * X + 1))
Inverse Cosine	Arccos(X) = Atn(-X / Sqr(-X * X + 1)) + 2 * Atn(1)
Inverse Secant	Arcsec(X) = 2 * Atn(1) – Atn(Sgn(X) / Sqr(X * X – 1))
Inverse Cosecant	Arccosec(X) = Atn(Sgn(X) / Sqr(X * X – 1))
Inverse Cotangent	Arccotan(X) = 2 * Atn(1) - Atn(X)
Hyperbolic Sine	HSin(X) = (Exp(X) – Exp(-X)) / 2
Hyperbolic Cosine	HCos(X) = (Exp(X) + Exp(-X)) / 2
Hyperbolic Tangent	HTan(X) = (Exp(X) – Exp(-X)) / (Exp(X) + Exp(-X))
Hyperbolic Secant	HSec(X) = 2 / (Exp(X) + Exp(-X))
Hyperbolic Cosecant	HCosec(X) = 2 / (Exp(X) – Exp(-X))
Hyperbolic Cotangent	HCotan(X) = (Exp(X) + Exp(-X)) / (Exp(X) – Exp(-X))
Inverse Hyperbolic Sine	HArcsin(X) = Log(X + Sqr(X * X + 1))
Inverse Hyperbolic Cosine	HArccos(X) = Log(X + Sqr(X * X – 1))
Inverse Hyperbolic Tangent	HArctan(X) = Log((1 + X) / (1 – X)) / 2
Inverse Hyperbolic Secant	HArcsec(X) = Log((Sqr(-X * X + 1) + 1) / X)
Inverse Hyperbolic Cosecant	HArccosec(X) = Log((Sgn(X) * Sqr(X * X + 1) + 1) / X)
Inverse Hyperbolic Cotangent	HArccotan(X) = Log((X + 1) / (X – 1)) / 2
Logarithm to base N	LogN(X) = Log(X) / Log(N)

 

Related topics

• Move
• Payload & Thrust