Die Mathematik hinter dem Optimizer |
Wie geht der Optimizer bei der Suche nach optimalen Parameterwerten bzgl. einer spezifischen Zielfunktion vor?
Es wird der Hill Climbing Algorithmus verwendet, welcher wie folgt vorgeht:
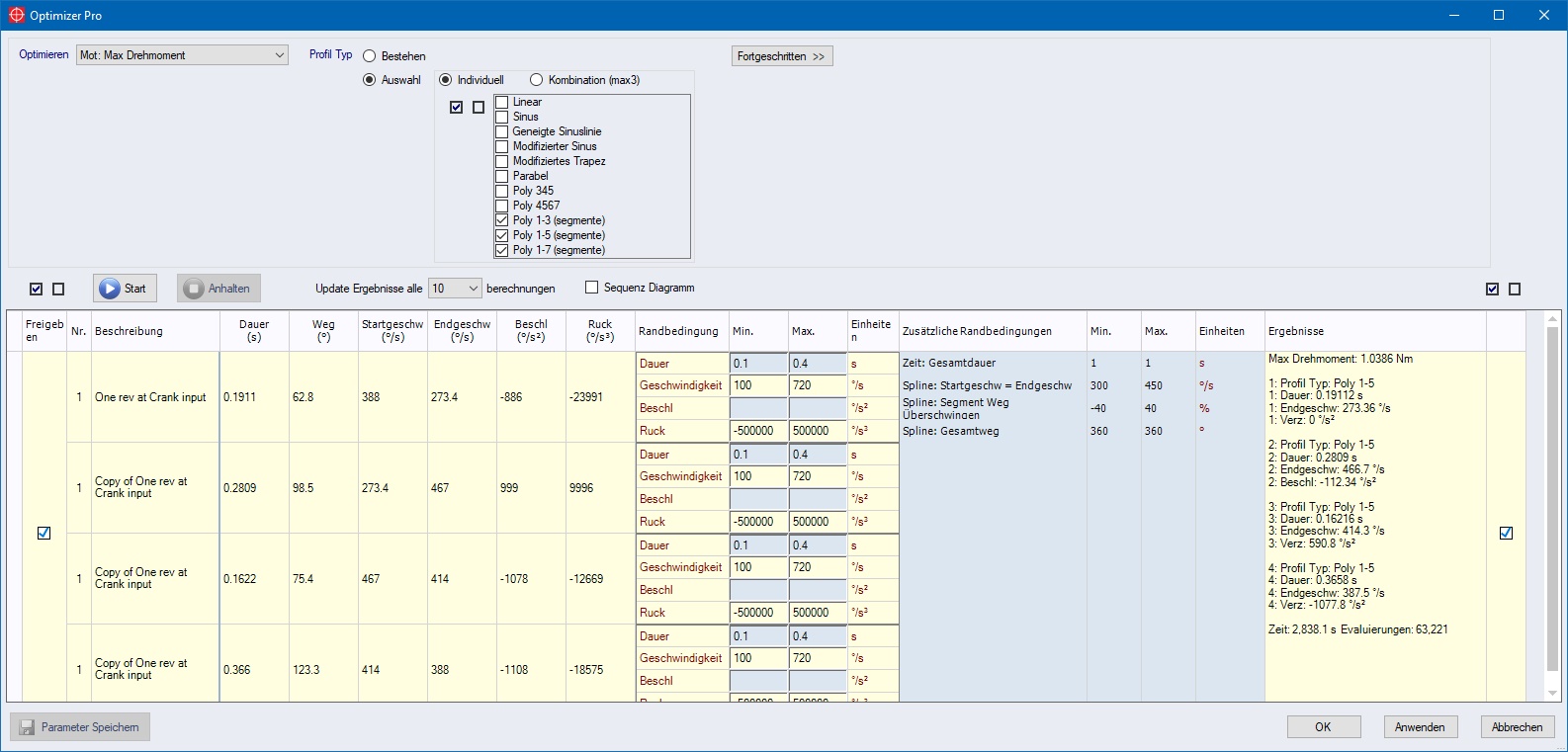
Aber wie starten wir mit einer Lösung, welche unsere Randbedingungen erfüllt? In den meisten Fällen erfüllt normalerweise die Lösung, mit welcher die Bewegung erstellt wurde, die Randbedingungen. Andernfalls muss der Optimizer nach einer Lösung, welche alle Randbedingungen erfüllt, suchen.
Und dabei kommt die “Populationsgröße” ins Spiel, welche dem Optimizer sagt, wie viele Startlösungen gesucht werden sollen. Eine zulässige Startlösung wird dabei jeweils durch Setzen von zufälligen Eingabeparameterwerten gesucht.
Beachten Sie, dass wenn die “Populationsgröße” auf Null gesetzt wird, dann verwendet der Optimizer nur Ihre vordefinierten Parametereinstellungen als Startlösung. Setzt man z.B. die “Populationsgröße” auf 10, dann verwendet der Optimizer Ihre vordefinierten Parametereinstellungen und 10 zufällig erzeugte Parametereinstellungen als Startlösungen.
Falls der Optimizer keine zulässige Startlösung finden kann, dann wird er nach mehreren Versuchen, durch den Wert “Max Anzahl unzulässiger Lösungen” angegeben, stoppen.
Für jede gefundene Startlösung wendet der Hill Climbing Algorithmus die Schritte 2 und 3 an.
Aber was bedeutet für den Hill Climbing Algorithmus in Schritt 2 “Nehme diese Lösung und verbessere sie”?
Dieser Schritt gibt dem Hill Climbing Algorithmus seinen Namen. Gehen wir zum Beispiel von einer zweiparametrigen Zielfunktion z = f(x, y) wie hier gezeigt aus:
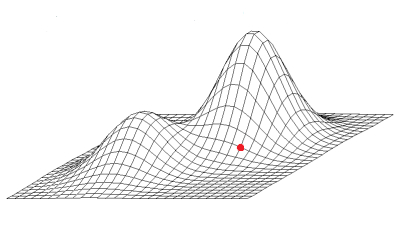
Mit einer Startlösung am rot markierten Punkt schaut der Hill Climbing Algorithmus nach, in welcher Richtung es bergauf geht, d.h. in welcher Richtung die Zielfunktion höhere Werte hat, falls er maximieren soll (soll er minimieren nimmt er einfach die negative Zielfunktion und maximiert).
Die Schritte 2 und 3 werden wiederholt angewandt bis der Hill Climbing Algorithmus ein lokales Maximum erreicht.
Mit der “Schrittweite Dauer”, “Schrittweite Geschw”, “Schrittweite Beschl” und “Schrittweite Ruck” können Sie die Genauigkeit am Gipfel, bzw. wann der Optimizer die Suche beenden soll einstellen. D.h. er hält an, wenn er noch genauere Schritte machen müsste, um eine bessere Lösung zu finden. Deshalb wird eine lokal optimale Lösung immer innerhalb der Genauigkeit Ihrer vorgegebenen Parameterschrittweite gefunden.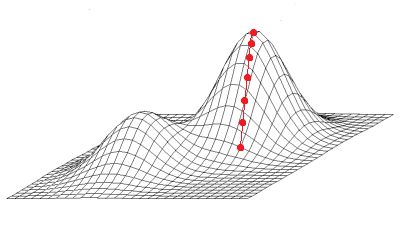
Da der Hill Climbing Algorithmus nur ein lokales Maximum findet, kann es sein, dass das nicht das höchste Maximum ist, z.B. wenn er eine ungünstige Startlösung verwendet:
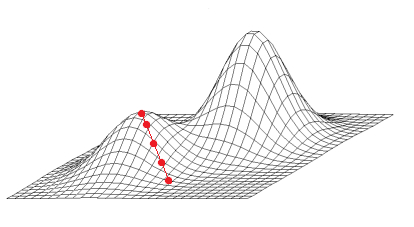
That’s why the Optimizer suggests always a certain “Population Size”, which corresponds one to one to the number of starting solutions to be used. Of course the Optimizer then compares all found local maxima and returns the highest.
Daher schlägt der Optimizer immer eine gewisse “Populationsgröße” vor, welche eins zu eins der zu verwendenden Anzahl an Startlösungen entspricht. Natürlich vergleicht der Optimizer dann alle gefundenen lokalen Maxima und gibt das Höchste zurück.
Vielleicht fragen Sie sich, wie kann man dann sicher sein, das globale Optimum zu finden?
Die Antwort ist, man kann sich nicht sicher sein, das globale Optimum zu finden, denn es gibt keinen mathematischen Algorithmus, welcher das garantieren könnte (nicht einmal, dass es mit einer hohen Wahrscheinlichkeit gefunden werden könnte). Je höher jedoch die "Populationsgröße", desto höher die Wahrscheinlichkeit, das globale Optimum zu finden.
Bei allen Ansätzen wird daher generell nach lokalen Optima gesucht und diese werden dann verglichen. Ein sehr guter und schneller Ansatz ist der Hill Climbing Algorithmus, welcher vollständig und elegant im SERVOsoft Optimizer integriert ist.