Polynome

Warum haben wir eine solch angeblich komplizierte Funktionalität in SERVOsoft integriert? Die Antwort ist, mit Polynomen können wir nahezu jede Bewegungsaufgabe lösen, und sie stellen eine der Grundlagen des Optimizers dar.

Also lassen Sie uns mit ein bisschen Mathematik beginnen und wir werden bald erkennen, dass wir uns am Ende auf unsere Bewegungsaufgabe und unsere bekannten Variablen Zeit, Weg, Geschwindigkeit, Beschleunigung, Ruck usw. konzentrieren können, wobei alle notwendigen Berechnungen automatisch von SERVOsoft ausgeführt werden.

Definition

Ein Polynom (n-ter Ordnung) ist eine mathematische Funktion der Form

Nomenklatur

Oft wird der Begriff "Polynom" mit "Poly" abgekürzt, und die Bezeichner werden mit "Poly 1-3", "Poly 1-5" und "Poly 1-7" abgekürzt. Polynome 345 und 4567 sind Teilmengen der vollständigen Polynome mit den ersten Termen auf Null gesetzt. Poly 345 und 4567, welche schon von Anfang an in SERVOsoft Verwendung finden, sind 'Rampen'-Profile, bei welchen Start- und Endbeschleunigungswerte immer Null sind.

Poly 1-5 und Poly 1-7, welche auch diese ersten Terme enthalten, sind wesentlich flexibler. Zum Beispiel kann der Anwender beim Poly 1-5 sowohl die Start- und Endgeschwindigkeit als auch die Start- und Endbeschleunigung vorgeben. Und beim Poly 1-7 kann der Anwender auch noch die Start- und Endruckwerte festlegen.

Bei n = 5 oder 7 wird das Polynom auch als "Polynom 5. Grades" oder "Polynom 7. Grades" bezeichnet. Weil SERVOsoft auch die 'Rampen'-Polynome 345 und 4567 verwendet, werden durch diese Namenskonvention eindeutig die verwendeten Terme angezeigt. D.h. man hat entweder "Poly 345", welches das 'Rampen'-Profil bezeichnet, oder "Poly 12345", welches alle Terme enthält.

Einfacher Einstieg

Aber fangen wir einfach an, das Polynom 1. Grades ist gemeinhin als Gerade bekannt

Wenn wir x als Zeit und p(x) als Verfahrweg betrachten, dann sieht ein Segment zum Beispiel so aus

mit und

 

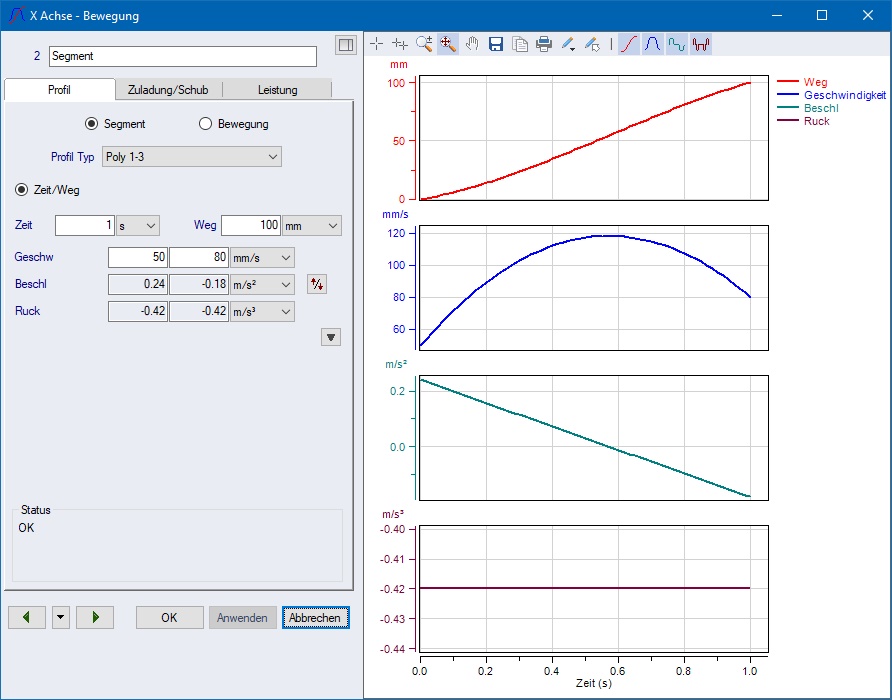
Aber wie Sie sehen können wird das Segment in SERVOsoft als Polynom 123, was ein Polynom 3. Ordnungbedeutet, mit den vier Variablen Zeit, Weg, Start- und Endgeschwindigkeit definiert.

Aber wie kommt es, dass so unsere Gerade definiert wird? Nun zunächst, wenn wir uns mit einem Polynom 3. Ordnung beschäftigen, müssen wir herausfinden, welche Werte die vier unbekannten Koeffizienten   haben.

Erinnern wir uns an unseren Lineare Algebra-Unterricht, dann brauchen wir vier Gleichungen, um ein Gleichungssystem mit vier Unbekannten zu lösen (und wir können die Einheiten jeweils weglassen):

  (G1, d.h. wir starten bei  und )
  (G2, d.h. der Verfahrweg in  beträgt )
  (G3, d.h. die Startgeschwindigkeit beträgt )
  (G4, d.h. die Endgeschwindigkeit beträgt )

      
Führen wir es einmal im Detail aus (beachten Sie dabei, dass wir in jeder neuen Zeile die Ergebnisse der vorangegangenen Zeilen schon berücksichtigen):

 

  (G1)        
  (G3)        
  (G2)       (eqn2a)
  (G4)       (eqn4a)


3 * (eqn2a)  –  (eqn4a)     ->          und mit (eqn2a)     ->     


Und es kommt heraus , und das ist die Gleichung unserer eindeutigen Geraden.

Dies führt uns zu unserem ersten Satz, der unser Leben beim Umgang mit Polynomen sehr vereinfachen wird. Denn in der Linearen Algebra gilt: Um ein Gleichungssystem mit einer Anzahl Unbekannter zu lösen benötigt man dieselbe Anzahl an Gleichungen, d.h. für eine Polynom 3. Ordnung mit vier unbekannten Koeffizienten werden wir vier Gleichungen, oder allgemein gesprochen Randbedingungen, benötigen.

Ein Polynom n-ter Ordnung ist eindeutig durch n+1 Randbedingungen bestimmt

Dieser Satz besagt, dass wir nichts über Koeffizienten zu wissen brauchen. Wir müssen nur unsere Anwendung und ihre Randbedingungen kennen, um Polynomsegmente zu definieren, die benötigten mathematischen Berechnungen werden alle von SERVOsoft automatisch gemacht:

  1. Für ein Polynom 3. Ordnung (Polynom 123) müssen wir also 4 Werte vorgeben
  2. Für ein Polynom 5. Ordnung (Polynom 12345) 6 Werte
  3. Für ein Polynom 7. Ordnung (Polynom 1234567) 8 Werte

Polynom 3. Ordnung (Polynom 123)

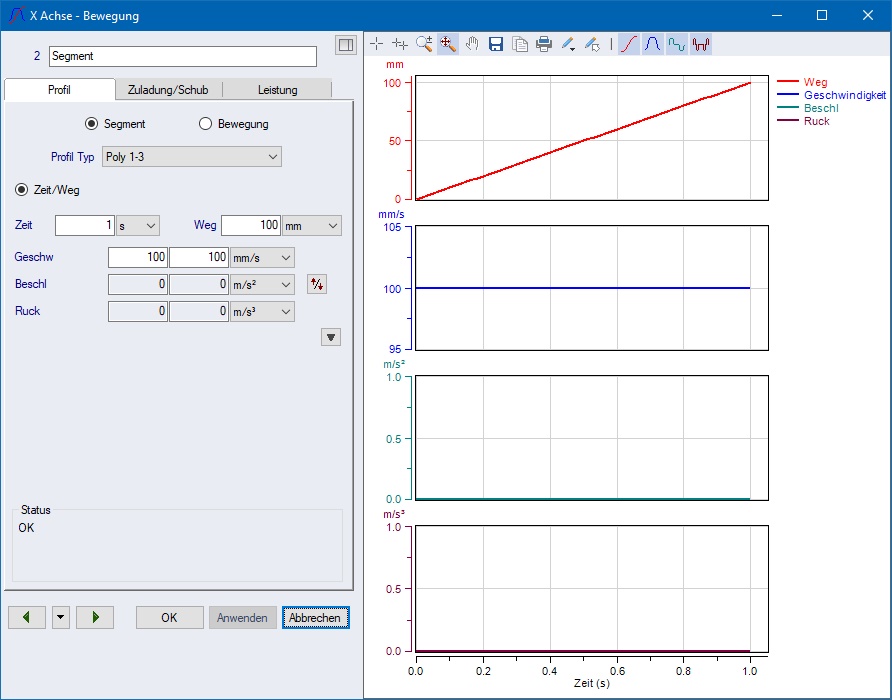
Zum Beispiel sieht ein Polynom 3. Ordnung mit den vier vorgegebenen Werten Zeit = 1 s, Weg = 100 mm, Startgeschwindigkeit =  und Endgeschwindigkeit =  eindeutig so aus:

Polynom 5. Ordnung (Polynom 12345)

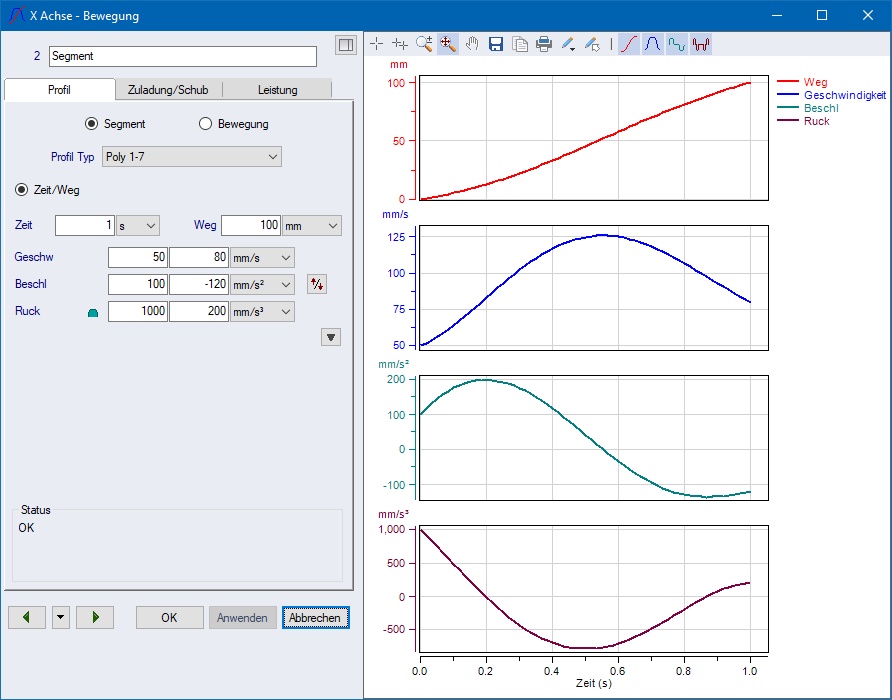
Ein Polynom 5. Ordnung mit den sechs vorgegebenen Werten Zeit = 1 s, Weg = 100 mm, Startgeschwindigkeit = , Endgeschwindigkeit = , Startbeschleunigung =  und Endbeschleunigung = eindeutig so aussehen:


Polynom 7. Ordnung (Polynom 1234567)

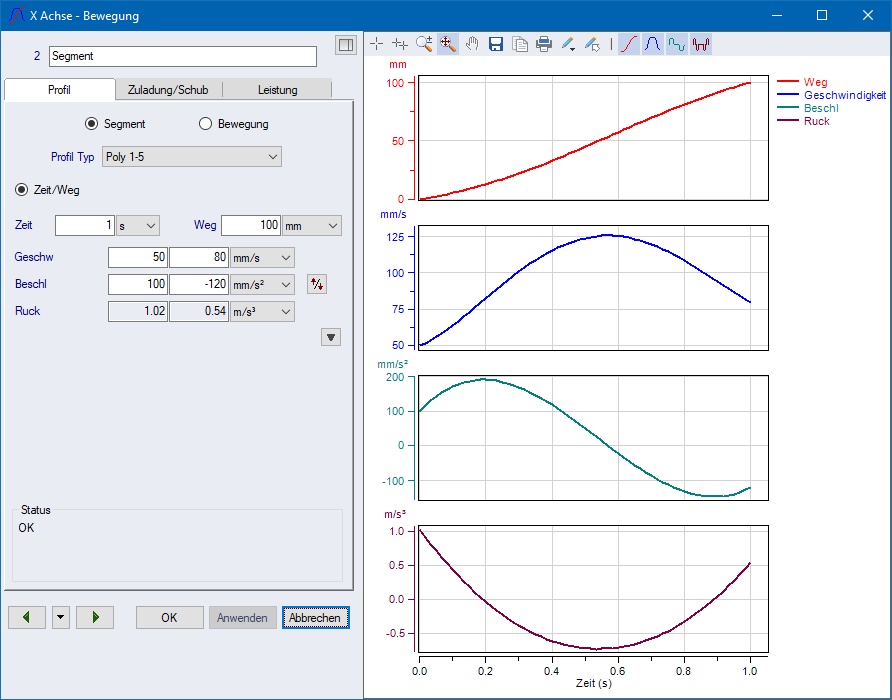
Ein Polynom 7. Ordnung mit den acht vorgegebenen Werten Zeit = 1 s, Weg = 100 mm, Startgeschwindigkeit = , Endgeschwindigkeit = , Startbeschleunigung = , Endbeschleunigung = , Startruck =  und Endruck =  wird eindeutig so aussehen:


 Verwandte Themen