Splines

Erinnern wir uns an die einfache Erstellung von Polynomen, d.h.

Dann können wir uns fragen, ob es nicht auch möglich ist, zusammengesetzte Polynome in ähnlicher Weise zu definieren? Denn beim Zusammensetzen einer Bewegung aus sagen wir 3 Polynomen 3. Ordnung müssten wir eigentlich 3 * 4 = 12 Werte vorgeben. Und das ist eine Menge, also warum lassen wir nicht einen Algorithmus die Arbeit für uns tun?

Definition

Eine Spline besteht aus zusammengesetzten Polynomen. Wenn alle Polynome 3. Ordnung sind, dann ist es ein kubischer Spline, wenn 5. Ordnung dann ein quintischer Spline und wenn 7. Ordnung dann ein septimischer Spline

Einfacher Einstieg

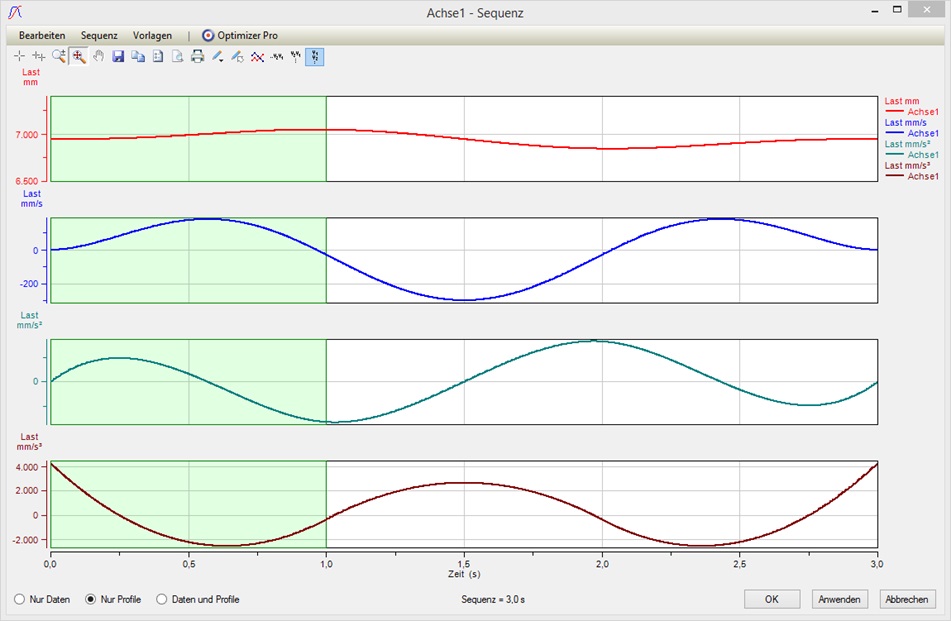
Aber fangen wir einfach an mit einem Spline bestehend aus 3 Segmenten, jedes ein Polynom 3. Ordnung mit jeweils Zeit = 1 s, Start-/Endgeschwindigkeit =  und das erste mit Weg = 100 mm, das zweite mit Weg = -200 mm und das dritte mit Weg = 100 mm.

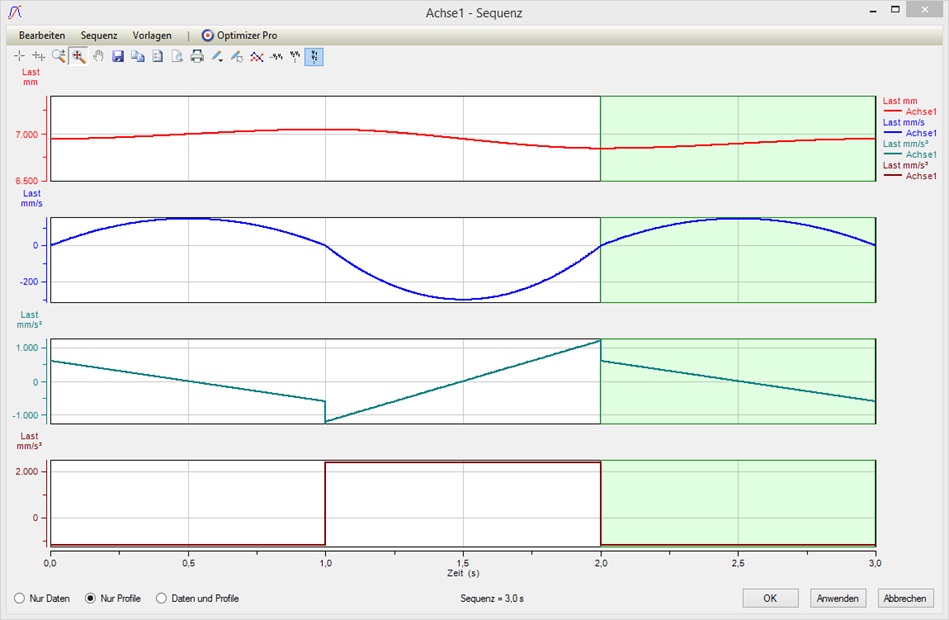
Sieht man sich das Profil genauer an, dann fällt auf, dass wir an den Übergangspunkten der 3 Segmente jeweils Beschleunigungssprünge haben. Diese rühren daher, dass die Polynome ja eindeutig aus den vorgegebenen Randbedingungen definiert sind. Um die Beschleunigungssprünge loszuwerden würden wir jetzt normalerweise anfangen, mit den Start-/Endgeschwindigkeiten an den Übergangspunkten zu spielen, dies händisch zu tun kann aber auf Dauer sehr mühsam werden.

Aber mit unserer einfachen Lösung bei Polynomen als Hintergedanke hilft uns jetzt noch ein Satz aus der Linearen Algebra weiter.

Ein Spline aus n Segmenten ist eindeutig definiert durch 2 * n Randbedingungen plus 2 falls er kubisch, plus 4 falls er quintisch, und plus 6 falls er septimisch ist

Das bedeutet im Detail:

Und dann lassen wir die integrierten Spline-Algorithmen eine Kurve mit glatten Übergängen an den Übergangspunkten der Segmente automatisch berechnen.

Kubische Splines

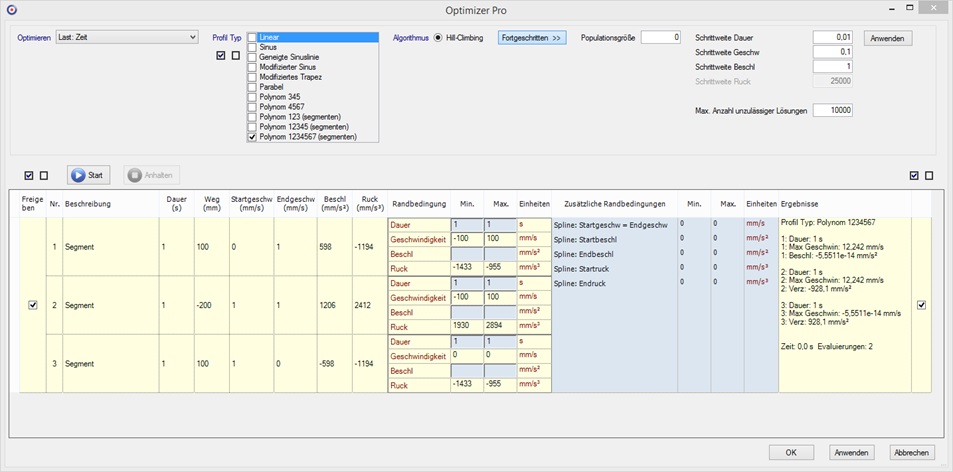
Diese können einfach mit dem Optimizer und Einstellungen wie hier gezeigt berechnet werden:

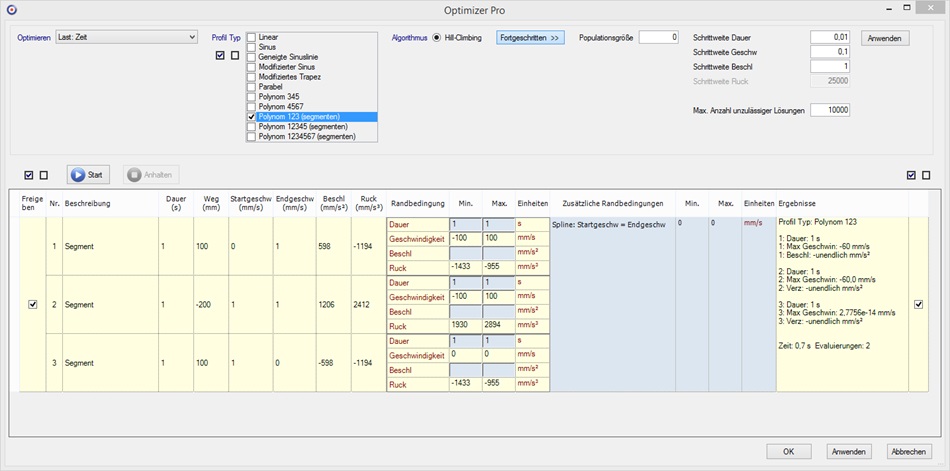
In diesem Beispiel verwenden wir den Optimizer nicht, um auf ein bestimmtes Ziel hin zu optimieren. Stattdessen halten wir alle freien Variablen fest mit unseren vorgegebenen Werten, z.B. setzen wir die Dauer jedes Segments fest mit Min und Max auf 1 s und verwenden die zusätzliche Randbedingung “Spline: Startgeschwindigkeit = Endgeschwindigkeit”, auch mit Min und Max fest auf ) gesetzt.

Dann lassen wir den Optimizer einen kubischen Spline mit den Einstellungen “Polynom 123 (Segmente)” und “Populationsgröße” gleich Null (wir wollen ja nicht optimieren) berechnen.

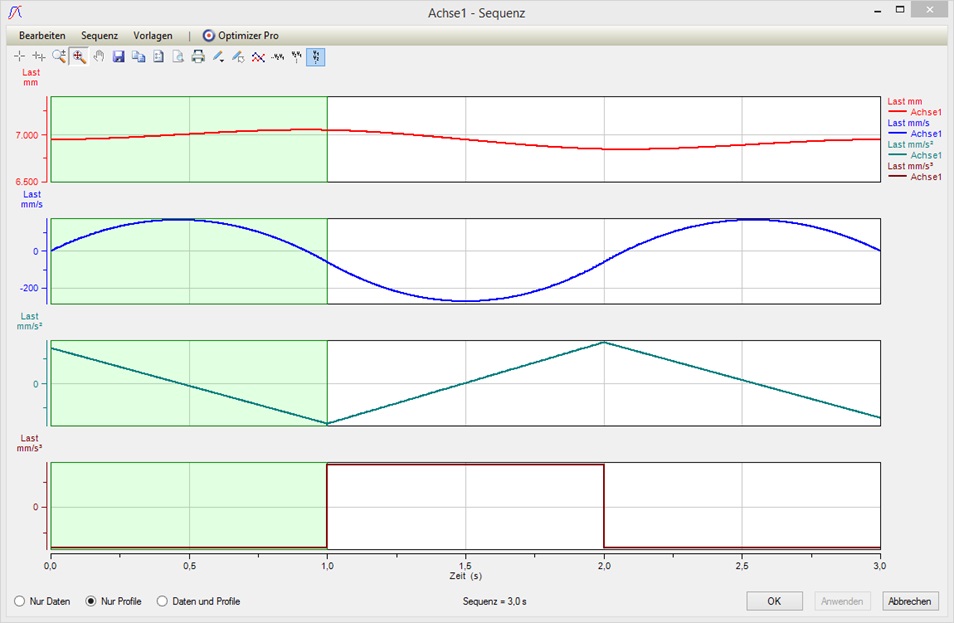
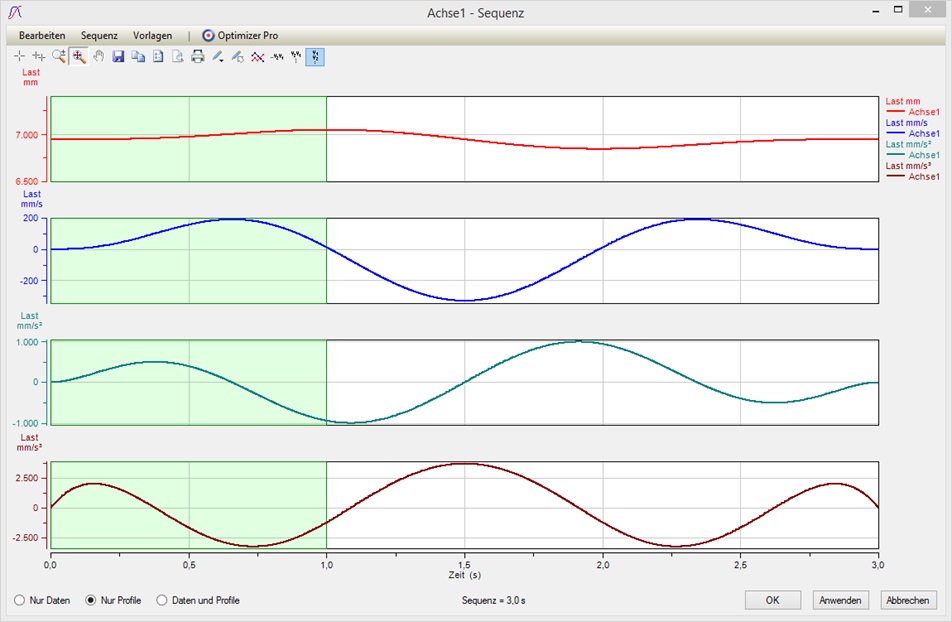
Nach Anwendung des Ergebnisses sehen wir, dass ein eindeutiger kubischer Spline berechnet wurde, welcher an den Übergangspunkten der Segmente stetig in Weg, Geschwindigkeit und Beschleunigung ist. Wir erhalten also eine insgesamt glatte Bewegung:

Quintische Splines

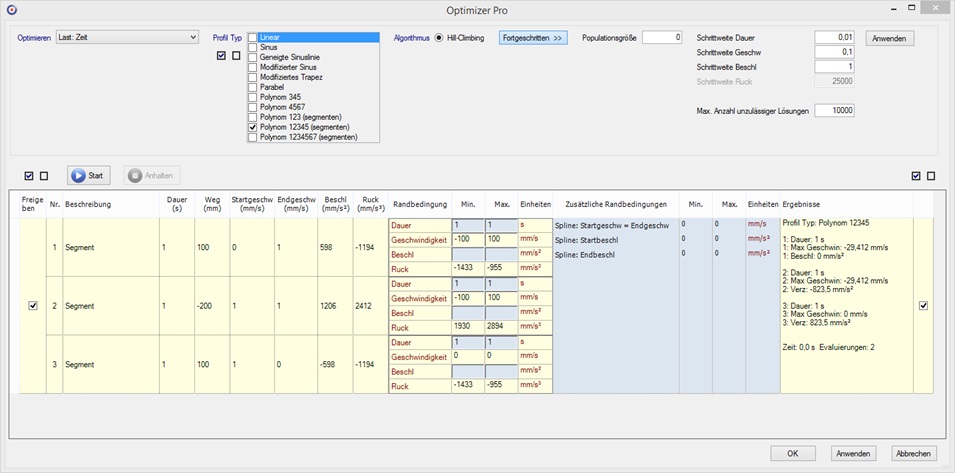
Natürlich können wir die Bewegung auch mit einem quintischen Spline realisieren. Dazu müssen wir “Polynom 12345 (Segmente)” und noch zusätzlich die Zusätzliche Randbedingungen “Spline: Startbeschleunigung” und “Spline: Endbeschleunigung”, mit Min und Max jeweils fest auf gesetzt, auswählen.

Und bei quintischen Splines sind auch noch die 3. Ableitung (“Ruck”) sowie die 4. Ableitung (“Ping”, “Klingeln” oder “Nachfedern”) stetig, wodurch noch weichere Bewegungen als mit kubischen Splines erzielt werden können.

Septimische Splines

LUnd nicht zuletzt können wir die Bewegung auch mit einem septimischen Spline realisieren. Dazu müssen wir “Polynom 1234567 (Segmente)” und noch zusätzlich die Zusätzliche Randbedingungen “Spline: Startruck” und “Spline: Endruck”, mit Min und Max jeweils fest auf gesetzt, auswählen.

Und bei septimischen Splines sind weiter noch die 5. Ableitung (“Knacken”) sowie die 6. Ableitung stetig, wodurch Schwingungen gedämpft werden. Zudem ist auch ein ruckfreier Bewegungsstart und ein ruckfreies Bewegungsende realisierbar.

Die Mathematik hinter den Splines

Was macht eigentlich der Optimizer beim Berechnen eines Splines?

Erinnern wir uns, dass ein Polynom 3. Ordnung so definiert ist:

Dabei müssen die vier Unbekannten  bestimmt werden. Also benötigen wir für ein Polynom 3. Ordnung vier Gleichungen, welche zusammen gelöst werden müssen.

Betrachten wir einen kubischen Spline aus sagen wir 3 Segmenten, dann müssen wir ein Gleichungssystem mit 3 * 4 = 12 Gleichungen lösen. Aber bei einem kubischen Spline aus 3 Segmenten müssen wir nur 2 * 3 + 2 = 8 Werte (Zeiten und Wege der Segmente + Start-/Endgeschwindigkeit des gesamten Splines) vorgeben.

Also wo bekommen wir die 4 fehlenden Gleichungen her?

Diese erhalten wir, wenn wir an den Übergangspunkten der Segmente jeweils Stetigkeit in den ersten und zweiten Ableitungen fordern. In unserem Beispiel oben, wo jedes Segment mit 1 s Zeit definiert war, bedeutet das für

 

  stetige Geschwindigkeitsübergänge   and
  und für stetige Beschleunigungsübergänge   and  

Mit diesen Forderungen können wir nun ein Lineares Gleichungssystem (LGS) aufstellen und lösen. In unserem Beispiel hier muss ein 12 x 12 Matrix-LGS gelöst werden.

 

Im Allgemeinen gilt:

  1. bei einem kubischen Spline aus n Segmenten ist eine (4*n) x (4*n) Matrix erforderlich
  2. bei einem quintischen Spline aus n Segmenten ist eine (6*n) x (6*n) Matrix erforderlich
  3. bei einem septimischen Spline aus n Segmenten ist eine (8*n) x (8*n) Matrix erforderlich

Natürlich erledigt dabei der SERVOsoft Optimizer alle Aufgaben und löst die Linearen Gleichungssysteme numerisch.


 Verwandte Themen