Optimizer Example Using the Slider Crank |
As explained in the Polynomials page:
And as explained in the Splines page:
These are a lot of parameters to set up for our motion tasks. And even if we do not deal with polynomials and splines, we have the motion parameters to set up, including times, distances and ramp parameters like velocities, accelerations and jerks.
But often we are actually not interested in the values of these parameters as long as they remain in a certain range.
For example if we want to downsize a drive chain, why not let SERVOsoft adjust the motion sequence in order to say, minimize the maximum motor torque? This is what the Optimizer can do for us.
The Optimizer automatically solves for input values in order to minimize/maximize a specific value, taking into account constraints for the input values and optionally constraints for additional output values.
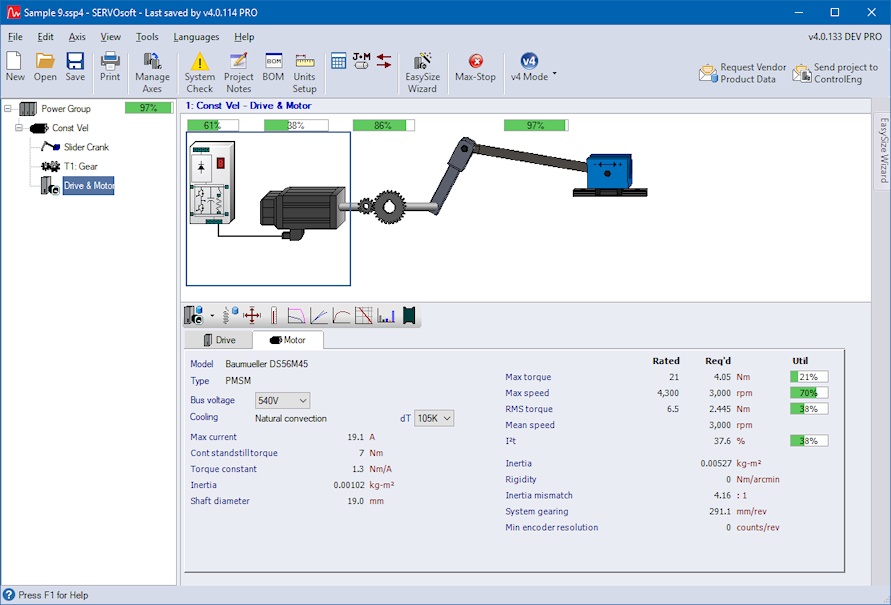
Let’s start simple with a slider crank example where the motor turns at constant speed of 3000 rpm, which via a gear ratio drives the crank arm at a constant velocity of 1 rev/s. So the slider moves back and forth and back and forth and so on as shown below. For this task we need a motor providing at least 4.07 Nm maximum torque.
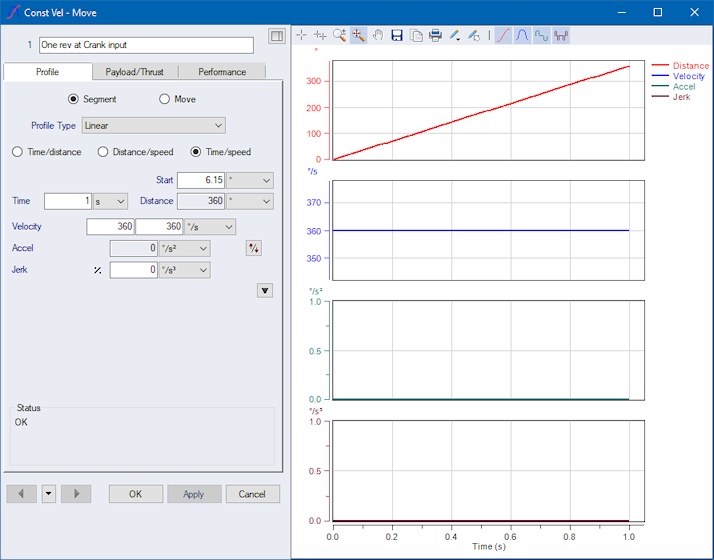
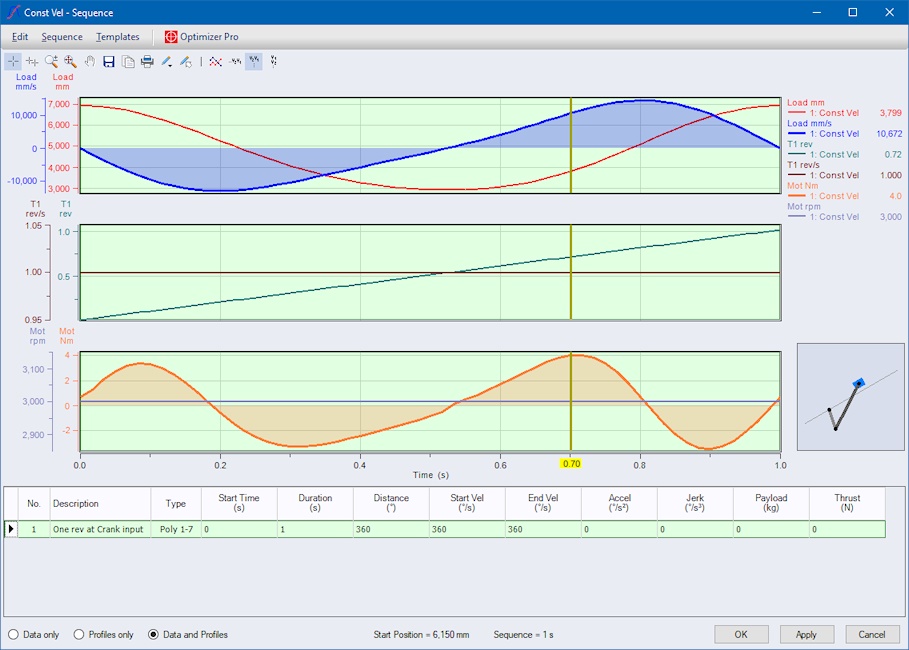
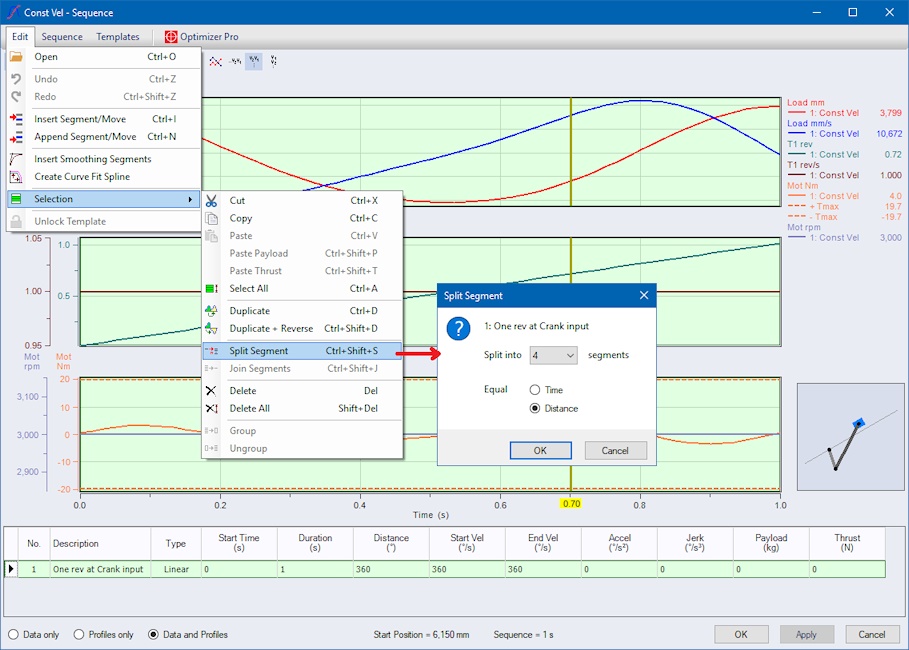
To give the Optimizer flexibility for minimizing the needed maximum motor torque, we first split up our movement into four segments, each turning 90° in 0.25 seconds. We could have split up in fewer or more segments, but four is a good choice based on experience. More segments provide even more flexibility for the Optimizer, and therefore can take longer to process.
As you can see the movement stays the same as before.
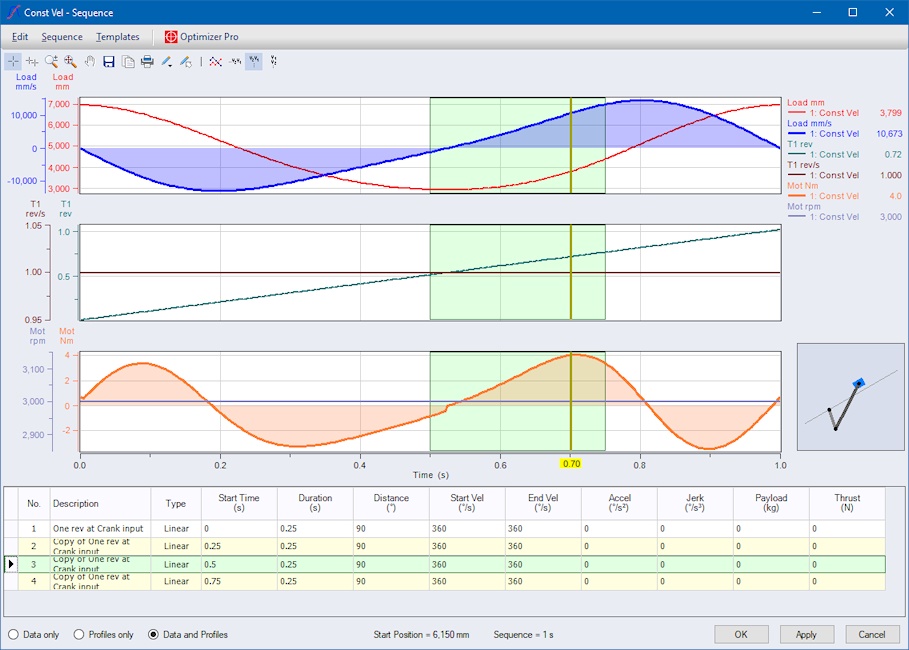
After pressing the “Optimizer Pro” button we are able to set up the target and all constraints for our parameters. We select to optimize for “Mot: Max Torque” using a quintic spline consisting of “Polynomials 12345 (segments)” and set the additional constraints as shown here:
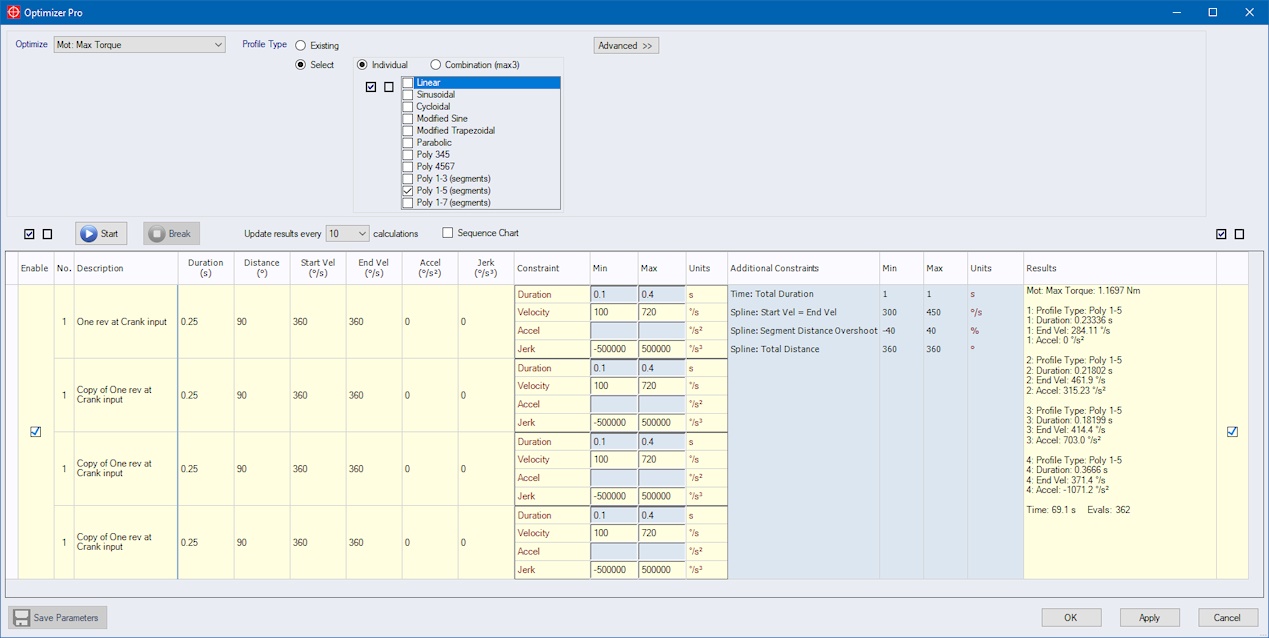
After pressing “Start” the Optimizer runs for approximately 1 minute searching for adequate durations for each segment, all the time looking out for a lower maximum motor torque.
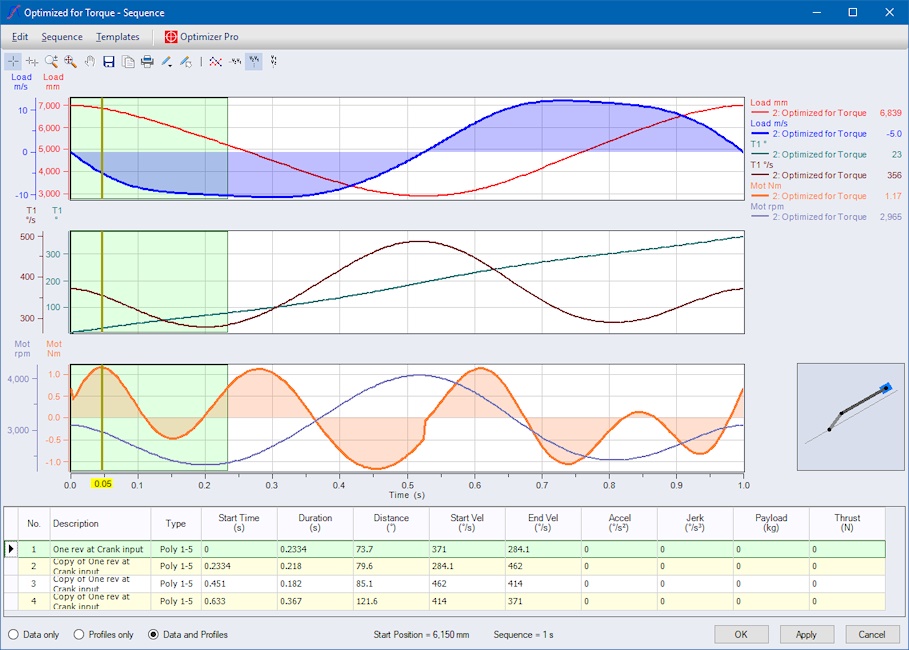
And as a result a quintic spline movement is found which, when driven at the crank arm, results in a maximum needed motor torque of approximately 1.5 Nm, which is more than 60% lower than what was needed when rotating at constant speed. Taking a closer look at the crank arm’s velocity profile, it now reduces speed every time the slider reaches its inner or outer limit (this is where the high torque was needed before).
Of course the slider still moves just back and forth and back and forth and so on. When you take a look at the drive and motor utilizations, they also decreased from 61% to 4% and 38% to 14%, respectively, which allows downsizing of the drive and motor.
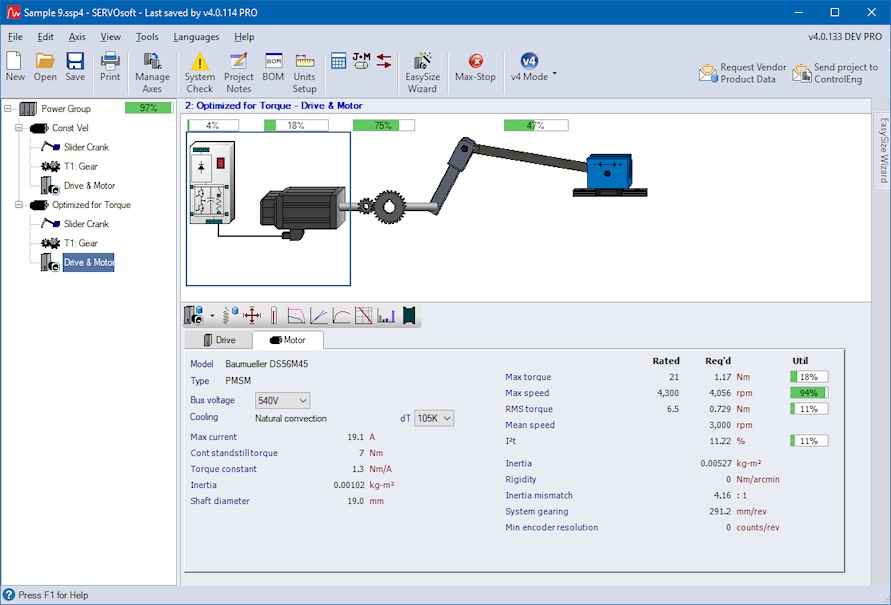
Asking if a motion control system is able to drive such a spline curve, we explicitly choose polynomials in SERVOsoft for motion design. Because every modern motion control system with cam ability can do the task using a virtual master axis moving at constant speed of 1 rev/s, and the crank arm moving as cam follower axis using the four polynomial segments of the automatically optimized quintic spline.