The Math Behind the Optimizer

What does the Optimizer do when searching for optimal parameter values regarding your specific target function?

Actually it uses the Hill Climbing algorithm which does following:

  1. Starts with a solution that meets the constraints
  2. Takes the solution and makes an improvement upon it
  3. Repeatedly improves the solution until no more improvements are necessary/possible

But how do we start with a solution that meets our constraints? In most cases, the solution you set up the movement normally meets the constraints. Otherwise the Optimizer has to search for a solution that meets the constraints.

And the “Population Size” is used to tell the Optimizer how many starting solutions it should look for by randomly setting the input parameter values in order to get a feasible starting solution.
Keep in mind when setting the “Population Size” to zero the Optimizer only uses your predefined parameter settings as starting solution. If setting the “Population Size” for example to 10, the Optimizer uses your predefined parameter settings and 10 randomly generated parameter settings as starting solutions.

If the Optimizer can’t find a feasible starting solution, it will stop after several tries specified by the “Max Infeasible Solutions” value.

For each found starting solution, the Hill Climbing algorithm works through steps 2 and 3. But what does the Hill Climbing algorithm do in step 2 “Takes the solution and makes an improvement upon it”? This step gives the Hill Climbing algorithm its name. For example considering a two parameter target function z = f(x, y) as shown here:

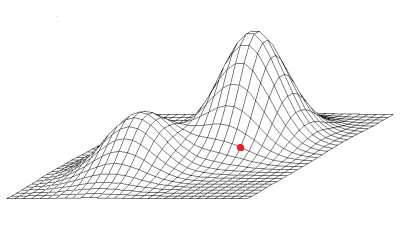
With a starting solution at the red dot, the Hill Climbing algorithm looks for the uphill direction, i.e. where the target function has a higher value when maximizing (when minimizing it just takes the negative target function and maximizes).

Steps 2 and 3 are repeated until the Hill Climbing algorithm reaches a local maximum.

With the “Dur Step”, “Vel Step”, “Accel Step” and “Jerk Step” you are able to set the accuracy at the top, telling the Optimizer to stop searching, i.e. it stops when it would have to make more accurate steps to achieve a better solution. Therefore a local optimal solution is always found within your given parameter steps accuracy.

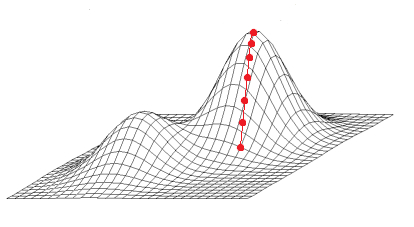
Since the Hill Climbing algorithm only finds a local maximum it might not find the highest maximum, for example when using an unfavorable starting solution:

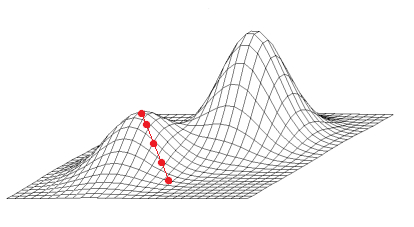
That’s why the Optimizer suggests always a certain “Population Size”, which corresponds one to one to the number of starting solutions to be used. Of course the Optimizer then compares all found local maxima and returns the highest.

So you might ask, how can I then be sure to find the global optimum? The answer is that you can’t be sure to find the global optimum, because there is no mathematical approach guaranteeing to find the global optimum (not even to find it with a very high probability). However, the larger the “Population Size”, the higher the probability to find the global optimum.

All approaches look in general for local optima and compare them. The Hill Climbing algorithm is a very good and fast approach, which is completely and elegantly integrated into the SERVOsoft Optimizer.

 


 Related topics